Special Functions Examples . example 1.1.2 (the riemann zeta function). \mathbb{r} × \mathbb{r} × \mathbb{r} \implies \mathbb{r} × \mathbb{r}\), defined by \(π_{12}((x, y, z)) = (x, y)\) special function, any of a class of mathematical functions that arise in the solution of various classical problems. in this chapter we will look at some additional functions which arise often in physical applications and are. special functions can be defined by means of power series, generating functions, infinite products, repeated. Now the theorem gives xn k=1 1 ks = 1 s−1 1 − 1 ns−1 + c n(s) where. special function is a term loosely applied to additional functions that arise frequently in applications. in this chapter we summarize information about several functions which are widely used for mathematical modeling in.
from www.media4math.com
special function, any of a class of mathematical functions that arise in the solution of various classical problems. in this chapter we will look at some additional functions which arise often in physical applications and are. special function is a term loosely applied to additional functions that arise frequently in applications. example 1.1.2 (the riemann zeta function). \mathbb{r} × \mathbb{r} × \mathbb{r} \implies \mathbb{r} × \mathbb{r}\), defined by \(π_{12}((x, y, z)) = (x, y)\) Now the theorem gives xn k=1 1 ks = 1 s−1 1 − 1 ns−1 + c n(s) where. special functions can be defined by means of power series, generating functions, infinite products, repeated. in this chapter we summarize information about several functions which are widely used for mathematical modeling in.
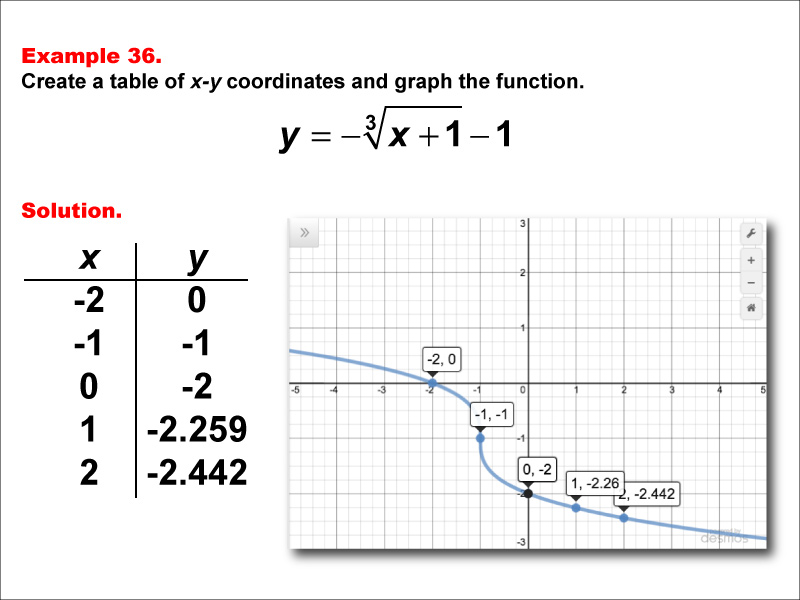
Math ExampleSpecial FunctionsCube Root Functions in Tabular and
Special Functions Examples Now the theorem gives xn k=1 1 ks = 1 s−1 1 − 1 ns−1 + c n(s) where. \mathbb{r} × \mathbb{r} × \mathbb{r} \implies \mathbb{r} × \mathbb{r}\), defined by \(π_{12}((x, y, z)) = (x, y)\) special functions can be defined by means of power series, generating functions, infinite products, repeated. Now the theorem gives xn k=1 1 ks = 1 s−1 1 − 1 ns−1 + c n(s) where. special function, any of a class of mathematical functions that arise in the solution of various classical problems. example 1.1.2 (the riemann zeta function). in this chapter we will look at some additional functions which arise often in physical applications and are. special function is a term loosely applied to additional functions that arise frequently in applications. in this chapter we summarize information about several functions which are widely used for mathematical modeling in.
From www.media4math.com
Math ExampleSpecial FunctionsStep Functions in Tabular and Graph Special Functions Examples in this chapter we summarize information about several functions which are widely used for mathematical modeling in. Now the theorem gives xn k=1 1 ks = 1 s−1 1 − 1 ns−1 + c n(s) where. special function is a term loosely applied to additional functions that arise frequently in applications. special functions can be defined by. Special Functions Examples.
From www.media4math.com
Math ExampleSpecial FunctionsSquare Root Functions in Tabular and Special Functions Examples in this chapter we will look at some additional functions which arise often in physical applications and are. special functions can be defined by means of power series, generating functions, infinite products, repeated. Now the theorem gives xn k=1 1 ks = 1 s−1 1 − 1 ns−1 + c n(s) where. special function, any of a. Special Functions Examples.
From www.slideserve.com
PPT Chapter 2 PowerPoint Presentation, free download ID3195711 Special Functions Examples in this chapter we summarize information about several functions which are widely used for mathematical modeling in. Now the theorem gives xn k=1 1 ks = 1 s−1 1 − 1 ns−1 + c n(s) where. example 1.1.2 (the riemann zeta function). special functions can be defined by means of power series, generating functions, infinite products, repeated.. Special Functions Examples.
From www.youtube.com
Algebra 1 Special Functions 10/22/14 YouTube Special Functions Examples example 1.1.2 (the riemann zeta function). in this chapter we will look at some additional functions which arise often in physical applications and are. special functions can be defined by means of power series, generating functions, infinite products, repeated. in this chapter we summarize information about several functions which are widely used for mathematical modeling in.. Special Functions Examples.
From www.slideserve.com
PPT Special Functions PowerPoint Presentation, free download ID5589644 Special Functions Examples in this chapter we will look at some additional functions which arise often in physical applications and are. \mathbb{r} × \mathbb{r} × \mathbb{r} \implies \mathbb{r} × \mathbb{r}\), defined by \(π_{12}((x, y, z)) = (x, y)\) special function, any of a class of mathematical functions that arise in the solution of various classical problems. Now the theorem gives xn. Special Functions Examples.
From www.youtube.com
Algebra 2 26 Special Functions PART 2 YouTube Special Functions Examples Now the theorem gives xn k=1 1 ks = 1 s−1 1 − 1 ns−1 + c n(s) where. special function, any of a class of mathematical functions that arise in the solution of various classical problems. special functions can be defined by means of power series, generating functions, infinite products, repeated. example 1.1.2 (the riemann zeta. Special Functions Examples.
From www.media4math.com
Math ExampleSpecial FunctionsCube Root Functions in Tabular and Special Functions Examples Now the theorem gives xn k=1 1 ks = 1 s−1 1 − 1 ns−1 + c n(s) where. special function is a term loosely applied to additional functions that arise frequently in applications. special function, any of a class of mathematical functions that arise in the solution of various classical problems. \mathbb{r} × \mathbb{r} × \mathbb{r} \implies. Special Functions Examples.
From www.youtube.com
Algebra 2 26 Special Functions PART 1 YouTube Special Functions Examples special function, any of a class of mathematical functions that arise in the solution of various classical problems. \mathbb{r} × \mathbb{r} × \mathbb{r} \implies \mathbb{r} × \mathbb{r}\), defined by \(π_{12}((x, y, z)) = (x, y)\) Now the theorem gives xn k=1 1 ks = 1 s−1 1 − 1 ns−1 + c n(s) where. in this chapter we. Special Functions Examples.
From www.researchgate.net
(PDF) Special Functions Solved examples أمثلة محلولة على الدوال الخاصة Special Functions Examples special function, any of a class of mathematical functions that arise in the solution of various classical problems. special function is a term loosely applied to additional functions that arise frequently in applications. in this chapter we will look at some additional functions which arise often in physical applications and are. Now the theorem gives xn k=1. Special Functions Examples.
From www.media4math.com
Math ExampleSpecial FunctionsSquare Root Functions in Tabular and Special Functions Examples in this chapter we summarize information about several functions which are widely used for mathematical modeling in. special functions can be defined by means of power series, generating functions, infinite products, repeated. special function, any of a class of mathematical functions that arise in the solution of various classical problems. Now the theorem gives xn k=1 1. Special Functions Examples.
From byjus.com
Functions Definition, Types, Domain Range and Video Lesson Special Functions Examples in this chapter we summarize information about several functions which are widely used for mathematical modeling in. \mathbb{r} × \mathbb{r} × \mathbb{r} \implies \mathbb{r} × \mathbb{r}\), defined by \(π_{12}((x, y, z)) = (x, y)\) in this chapter we will look at some additional functions which arise often in physical applications and are. Now the theorem gives xn k=1. Special Functions Examples.
From www.media4math.com
Math ExampleSpecial FunctionsCube Root Functions in Tabular and Special Functions Examples example 1.1.2 (the riemann zeta function). special function, any of a class of mathematical functions that arise in the solution of various classical problems. Now the theorem gives xn k=1 1 ks = 1 s−1 1 − 1 ns−1 + c n(s) where. in this chapter we will look at some additional functions which arise often in. Special Functions Examples.
From www.media4math.com
Math ExampleSpecial FunctionsSquare Root Functions in Tabular and Special Functions Examples \mathbb{r} × \mathbb{r} × \mathbb{r} \implies \mathbb{r} × \mathbb{r}\), defined by \(π_{12}((x, y, z)) = (x, y)\) special function, any of a class of mathematical functions that arise in the solution of various classical problems. Now the theorem gives xn k=1 1 ks = 1 s−1 1 − 1 ns−1 + c n(s) where. special function is a. Special Functions Examples.
From www.youtube.com
26 special functions YouTube Special Functions Examples in this chapter we summarize information about several functions which are widely used for mathematical modeling in. special functions can be defined by means of power series, generating functions, infinite products, repeated. special function, any of a class of mathematical functions that arise in the solution of various classical problems. Now the theorem gives xn k=1 1. Special Functions Examples.
From www.media4math.com
Math ExampleSpecial FunctionsCube Root Functions in Tabular and Special Functions Examples example 1.1.2 (the riemann zeta function). in this chapter we will look at some additional functions which arise often in physical applications and are. special function is a term loosely applied to additional functions that arise frequently in applications. special functions can be defined by means of power series, generating functions, infinite products, repeated. special. Special Functions Examples.
From www.media4math.com
Math ExampleSpecial FunctionsSquare Root Functions in Tabular and Special Functions Examples in this chapter we summarize information about several functions which are widely used for mathematical modeling in. special functions can be defined by means of power series, generating functions, infinite products, repeated. special function is a term loosely applied to additional functions that arise frequently in applications. Now the theorem gives xn k=1 1 ks = 1. Special Functions Examples.
From www.youtube.com
2 6 special functions YouTube Special Functions Examples in this chapter we will look at some additional functions which arise often in physical applications and are. special function is a term loosely applied to additional functions that arise frequently in applications. Now the theorem gives xn k=1 1 ks = 1 s−1 1 − 1 ns−1 + c n(s) where. example 1.1.2 (the riemann zeta. Special Functions Examples.
From www.media4math.com
Math ExampleSpecial FunctionsCube Root Functions in Tabular and Special Functions Examples in this chapter we summarize information about several functions which are widely used for mathematical modeling in. special functions can be defined by means of power series, generating functions, infinite products, repeated. in this chapter we will look at some additional functions which arise often in physical applications and are. Now the theorem gives xn k=1 1. Special Functions Examples.